空间句法方法：教学指南节选

摘要：《空间句法方法：教学指南》是伦敦大学学院的教材，关注建筑和城市空间的网络化表达，可读性强，并广受欢迎。本文选取了2016年1月最新更新的章节，力图介绍空间句法近期的发展，集中关注线段分析、高级的轴线和线段分析、以及它们的理论背景和教学实践。

该书的贡献者还包括：萨姆Ÿ格里菲思（Sam Griffiths）, 凯万·卡里米（Kayvan Karimi）, 劳拉·沃恩（Laura Vaughan）, 索菲亚·萨莉（Sophia Psarra）, 露丝·康罗伊·道尔顿（Ruth Conroy Dalton）, 塔索斯·瓦汝笛斯（Tasos Varoudis）, 克斯廷·塞勒（Kerstin Sailer）, 杨滔, 阿瓦·法塔赫·根·希克（Ava Fatah gen. Schieck）, 肖恩·汉纳（Sean Hanna）

线段分析的理论背景介绍

本章我们将诠释一种新的城市句法表达方式，可应用于分析空间的拓扑结构和几何结构。这种句法表达基于街道线段，考虑它们之间的拓扑连接、米制距离关联和角度变化。在其他软件的配合下，DepthmapX可进行不同半径、不同类型的线段分析。本章将介绍线段分析的相关内容，包括：线段分析的适用范围、其作为预测社会经济活动的强大功能、以及与之相关的不同尺度的变量和距离定义。此外，还将介绍这种线段分析的历史背景，以及这如何体现了空间句法理论中方法体系的范式变迁。轴线分析与线段分析区别将会加以明确。本章将重点强调街道网络中度量可达性的最有力变量，即半径限制下的角度深度。使用这种分析方法，学生们将会了解到，度量街道网络可达性时，存在两个图论中心性过程的变量，即整合度和选择度。其中，整合度和选择度是分别用来度量到达性交通与穿越性交通的潜力。本章最后将总结角度线段分析标准化的方法，这是由杨滔最初提出的。该方法使得我们能够比较不同城市和同一城市不同地点的句法分析结果。

线段模型：城市空间的线性表达

在之前的章节中，我们介绍了城市空间的轴线模型是如何帮助预测真实城市中的交通活动潜力的。然而，当试图检测系统中有类似连续性的街道时，轴线似乎显得不是那么有用。特别是在结构形态呈现一致性的城市中，只有极少的中断或线形街道与方格网街道斜交的情况下，例如曼哈顿的百老汇。在上述情况下，一种不同的空间结构表达很有必要（Dalton, 2001）。这种表达需要能够检测城市结构中的线性连接和半线性连接，因此应使用角度结构而非拓扑结构更为有效。为了达到这个目的，空间句法模型引入了一种更为精细的表达，它将街道线段视为街道网络的基本组成部分。每条街道线段被定义为轴线或街道两两交叉点之间的那部分。线段的表达方式可以基于轴线模型和道路中心线数据（Dalton et. al., 2003）。在大多数案例中，线段街道模型不同的表达只会对总体结构的理解造成微小的偏差（Dhanani et. al., 2012）。在城市边缘地区，这些偏差会变得比较明显（Hillier et. al., 2012）。因此，在做角度线段分析之前，需要对道路中心线数据进行清理。GIS中有一些简单的算法可以修正较小的半连续街道线段。

线段分析会处理街道网络的几何特性，累计每一对交叉的街道之间的角度。角度深度是一个最有用的结构分析方法，该方法可以描述空间网络中最小角度变化的路径。角度分析被认为可以很好地与空间导航和寻路行为相一致。因为当使用者行走在一个陌生的环境中，他们有可能最小化认知距离（Hillier & Iida, 2005）。

米制距离半径限制下的角度线段分析

前文提到过，米制距离半径限制下的角度分析有助于检测街道网络中主要的到达性交通和穿越性交通路径。研究表明，米制距离半径尤其有效，这可以避免一组预先选择的街道所形成的分区而引发的边界效应（Turner, 2001）。边界的选择可能会造成模型中的距离计算产生失真影响。

需要重点强调，米制距离半径的度量对应的是：在度量半径距离内从每条线段到达出发，沿所有街道扩展而得到的米制距离。按照这个定义，半径n就可以理解为：每条线段与城市中其他所有线段的关联过程之中，没有任何半径的限制。随着我们减小度量半径，模式也会随之改变。因此，如果我们把度量半径看作是在由节点和连接所组成的图论网络中的一个“饼干切割模具”，而这个图论网络就表示一个有线段和交叉点的线段模型，系统将只针对特定节点或线段进行分析。在这种情况下，400米半径（大约5分钟步行距离）将只计算由当前节点至400米范围内所有节点的角度变化，而不会计算任何超出这个半径范围之外的节点。这就意味着系统将只判断400米范围内线段元素与相邻线段之间的局部关系。

在分析中，半径最小值和最大值的选择不受特定标准的限制。在开始分析之前，应根据调查的本质提出一些基础研究问题：在一个确定的城市地区内，何种度量半径可以最优地反映如下内容：街区大小、线段长度、土地价值、推特活力、污染率、或观测的行人与机动车交通模式等。局部活动通常最好由800米（大约10分钟步行距离）局部度量半径表达。在更小街坊规模的市场地区，最好由更小的半径来表达，如400米。更大的度量半径则可更好地表达了机动车流量。

线段分析中角度深度的计算原则

线段模型就是轴线模型的碎片化表达，其中线段元素就是轴线模型中两两交叉点之间的部分（如果交叉线尾足够长，则可以保留）。从局部角度来看，线段模型显得相对有些无趣。因为线段连接着交叉点，它们一般性的连接度就是3或6。然而，在全局范围内分析时，根据系统（线段模型的角度分析）中每条线段到达其他线段经过转角的平均数量，城市环境的分析结果类似于轴线模型的整合度分析结构，不过更为精细。

希列尔（Hillier）和饭田（Iida）（2005）给出了线段模型中计算角度连接的方法。如果两条线段直线连接，则转角为0步。如果两条线段交角为90度，则转角为1步。而如果两条线段对折切呈相反方向（180度转角），则转角为2步。在角度分析中，两条线段的转角就是在0到2的范围内。图论中，转角“成本”被称为“加权”：任何一个连接都有相应的加权。因此，线段模型被称为加权模型。线段分析中，角度深度计算的形式与轴线分析中有所不同。线段角度深度的计算中，角度变化作为拓扑深度的加权值。

简单理解就是，如果两条线段交叉点的入射角度为47度，接近于45度，它的权重就是0.5。如果上述两条线段中的任意一条与第三条线段的交角为107度，则其权重为1。如果这三个线段元素同方向连接，那么这三个街道元素之间的角度深度就是它们交叉点角度加权之和，即0.5+1=1.5。这个角度总和可以理解为“图形中假定路程的成本”，其中“最短路径”代表了街道网络中从一条线段到其他所有线段的最小角度成本（Turner, 2001）。其中，转角我们始终认为它是正数，并且计算为定向运动。也就是说，从一条线段出发的点，其“下一步”连接的方向应该与“上一步”连接到达线段上该点的方向一致。

郁金香分析

郁金香分析的命名源于拉力赛车手导航时使用的地图。实际上，这些地图就是一系列简单的转弯图示。因此，司机（实际上是司机使用的导航）可以看到“左转”和“右转”，有时甚至知道转角的角度。这种表达也许对拉力赛车手并不是那么特殊，也许是合理的。然而，蒙特洛（Montello）（1991）认为我们根据那些分类才记住转弯，而Hillier（1999）提出我们的认知构建过程就是分类，这形成了一系列的转弯类型。此外，常识表明，我们通常会误解近似方格网的系统，在其中我们会认为那些路径是正交的，而实际上它们往往不是的（Hillier, 2003）。是否人们只能记住转弯的类型，而不能精确地记住转弯的角度？如果如此，那么相对于未分类的转弯分析，转弯类型的分析是否与交通模式有更好的相关性？DepthmapX提供了探究这些问题的平台。蒙特洛（Montello）发现，转弯可以大致以45度为单元，因此这样的分类也许是合理的：总共5个区间，如小于22.5度区间、22.5度至67.5度区间、67.5度至112.5度区间等。

郁金香分析的基本原则是将转弯角度近似为分段的圆。例如在8区间的郁金香分析中，360度等同于32个区间。下面的例子将说明郁金香分析是如何估算近似值的：

- 小于22.5度的转角赋值为0

- 22.5度至67.5度的转角可四舍五入为45度，赋值为0.5

- 同理，97.5度转角可四舍五入为90度，赋值为1。

这个赋值约定再次使用了希列尔（Hillier）和饭田（Iida）（2005）提供的标准角度分析的取值范围。这种分类方法也许是合理的。DepthmapX使任何角度的线段均可以在4到1024个区间的范围内取值。1024 个区间就近似于标准角度分析。而郁金香分析的优势在于，它的计算速度要比角度分析快得多。因为电脑不必花费时间用于决定一个转角的确切度数或是这个转角是否比另一个小，而是直接将转角分配到对应的区间上。对于合理规模的系统来说，用1024个区间的郁金香分析所计算平均角度深度和直接计算平均角度深度几乎是一样的。

高级的轴线分析与线段分析的理论背景——前景与背景分析介绍

本章旨在阐述城市中米制距离分析的部分相关内容，并说明在网格结构规模一致的情况下，该分析如何帮助识别城市分区。在线段模型中，这些分区呈现出拼贴模式（Patchwork Patterns）。通过这些拼贴地区，可以识别出高密度城市分区中局部的米制距离特性。本章还将会阐明全局性道路的主要作用，通过街道网络的拓扑几何特性可识别那些全局性道路。本章将详述街道结构中这两种线段特性。一方面，DepthmapX中的米制距离深度工具可用于模拟高密度拼贴模式，本章介绍其理论框架；另一方面，为了揭示网格的拓扑几何前景结构，本章还会回顾角度选择度和角度深度的相关内容。本章将简要论及街道结构的不同等级与高密度拼贴模式之间的潜在内在联系，这是极其复杂的。我们认为这类分析可以深刻理解街道网格的生成机制、以及社区聚集与社会进程的空间物化之间的内在关联。

城市中区分整体结构与局部结构的主要因素是什么？

城市可以用大型的模型网络来表达，其中街道空间的线性表达可以看做是节点，街道线之间的交叉点可以看做是连接。如果我们把街道交叉口看作是街道空间更精细的表达，也许我们就会对城市空间有更丰富的认知。以上这些就是线段模型的作用。通过对生成其结构的线性元素的阐释，线段模型可以帮助理解街道布局的复杂性，即降低理解的复杂程度。对街道线段结构的拓扑特性和几何特性进行分析，可以揭示一些生成城市网络的过程、以及不同经济社会因素在城市形态生成过程中的作用。在共时性的表达中，句法模型可以解释这些过程，同时还可以揭示局部简单的变化可生成全局性结构，这与城市结构相类似。对于局部动态变化的描述来自于希列尔（Hillier）（1996a）提出的“中心性和延伸性”：如果可以打断较短的街道，就不要去打断较长的街道。通过实施这个规则，我们可以得到一个庞大的聚集结构，其中短线以几近直角的方式相交，而连续交叉的长线之间的交角更小，并且与其他部分的局部结构相连接。均匀的短线构成了拼贴模式，嵌套于全局接近线性连接的网络之中。通过街道网络的米制距离特性和角度特性，可识别出局部街道结构的集合模式与主要道路设施的全局模式。

在定义街道网络的全局结构或前景网络方面，最初的句法轴线模型暴露了一些缺陷，因此对于方法学的更新是有必要的。菲格雷多（Figueiredo）和阿莫林（Amorim）（2004, 2005）早前的研究已经说明轴线分析不能识别系统中连续的线性关系。为了解决这个问题，菲格雷多（Figueiredo）和阿莫林（Amorim）提出把“连续线（continuity lines）”作为统一交角较小的较长轴线的方法，然后在计算空间句法不同结构参数时，可以把这些统一的连续线看做是单一的元素。基于这种方法，“连续线”可以展现网络的全局结构，并突出那些由于自身结构特性而承担较高交通流量的道路。达尔顿（Dalton）（2001）的研究曾涉及半连续性街道问题。他提出在计算城市布局拓扑深度时，使用分数分析来识别角度模型距离。通过使用分数分析，可以突出百老汇在曼哈顿方格街道网络中的作用。达尔顿（Dalton）（2007）的另一个贡献是，凭借经验定义了局部结构。他竭诚努力发现了一些有关城市特征的定量描述。达尔顿（Dalton）的方法是对轴线的点协同度（point synergy）和点可理解度（point intelligibility）的数值进行划分，相应地得到一个拼贴模式，这显示邻里周边的模糊边界。希列尔（Hillier）（1996）的研究认为协同度（synergy）就是局部整合度和全局整合度之间相关性的表达，这可以揭示一些城市中局部与整体结构之间的潜在关系。同样地，可理解度（intelligibility）是轴线模型中局部连接性和整合度之间的关系表达，这可以告诉使用者某个空间的可识别性和渗透性。

最近，希列尔（Hillier）、特纳（Turner）、杨滔（Yang）和帕克（Park）等（2009）的研究揭示了有关网格结构的局部和全局模式的有趣现象。局部模式体现为米制距离相似的拼贴地区；而全局模式则表达为网格中半连续线，这反映了城市系统中所有起点与终点间的最短路径。基于米制距离的拼贴模式作为背景网络，在一定程度上与行政确定的邻里局部地区相一致。度量的尺度对米制距离拼贴模式影响很大。较长连续线作为前景网络，这可以表示最短路径的连接。它们通常与城市结构中繁华路段非常匹配。

背景分析：生成拼贴模型

拼贴模型是城市结构中米制距离密度的有趣表达。它们看起来很有意思、并很有前景。这是由于它们可以划分出城市的不同地区（Hillier et. al., 2009）。这些拼贴模式的集合可以揭示连接、削减和扩散的局部动态过程的空间属性（Al_Sayed, 2013）。米制距离分析的意义、及其与角度分析的相关性都非常依赖于度量的尺度（见图2）。在步行尺度的半径距离内，米制距离分析非常近似于角度分析。随着半径的增加，我们可以发现米制距离距离与角度距离之间的相关性变得越来越弱。这就意味着，在全局尺度下城市网络的角度几何结构和米制距离几何结构也许强调了不同的特性。角度分析所揭示的重要路径往往与交通流相符。然而当使用米制度量分析时，分析结果与人车行交通的相关性并不强（Hillier et. al., 2009）。因此，需要重点强调的是米制距离分析并不适用于大尺度下的城市建模和预测。它更可能适用于强调局部半径内的可步行地区。在一定的米制距离半径的限制下，系统的平均米制距离深度通常可以揭示拼贴模型。因此，需要了解你所研究的局部地区，这非常重要。这是由于当半径较小时（以400米半径为例），拼贴模型会选择密集的局部结构中较小的斑块。随着米制距离半径增大，斑块就会越变越大。这样，在城市化区域内，大尺度半径就可以揭示规模更大的稀疏或紧凑的地区，然而这并没有交通和社会经济的内涵。例如，如果横坐标是城市系统中所有元素的平均米制距离深度，纵坐标是1000米半径限制的平均米制距离深度，那么我们从波峰和波谷的模式，可以看出米制距离定义下的局部地区的聚集程度。除此之外，还需要强调的是，街道结构的密度和不同半径的分析结果也与城市街区的布局和规模有关系。在空间系统的中心地区，随着街区块的缩小，街道结构增强，且平均米制距离深度降低。然而，当城市中心地区的街区逐渐变大时，结果完全相反。因此，我们认为城市中心往往是强化其网格密度，从而使深度最小化。

拼贴模型可以展现在规模和网络距离方面特性相似的区域，而有另一种模型则可以用于识别模型中的非连续性（Yang & Hillier, 2007）。杨滔的模型可以解释因城市系统中每个元素分析半径变化而造成的节点数的变化。空间网络会选择非连续性，而这反过来又与拼贴模型相似。一般来说，在决定局部网格结构的特性方面，米制距离深度和节点数都起到了至关重要的作用。然而随着分析尺度的扩大，它们的影响也随之减小。当分析半径非常大时，最能表现城市结构全局特性的是角度拓扑几何结构。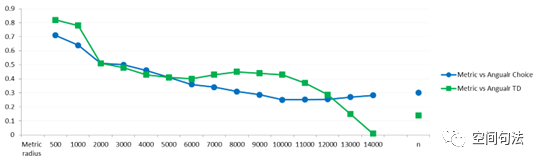

巴塞罗那中米制距离与角度距离之间的关系。一系列相关系数反映了在不同米制距离半径下，米制距离平均深度（MMD）与角度总深度之间的关系、以及米制距离平均深度（MMD）与选择度的关系。根据Al_Sayed, 2013进行编辑。

前景分析：生成拓扑几何分析

一组近似连续的线性连接通常可以揭示城市的全局结构，它们承载着所有起点与所有终点之间的最短历程。于是，将全局道路设施网络视为城市网格中独立的前景网络，这也许是合理的。正如我们所看到的，米制距离分析只能在局部小尺度半径下发挥作用，而全局半径通常是拓扑结构或拓扑几何结构。如果在小尺度半径限制下计算每条线段元素的平均米制距离深度或节点数，物理距离的结果就可以揭示局部结构（见图3）。然而，一旦增大分析半径，重叠效应就会出现（Hillier et. al., 2009）。每个单独元素周围的“缓冲区”之间会出现更多重叠。总体来说，很少需要直观的分析来计算系统中深度和出行成本之间的关系。

巴塞罗那的拼贴模式

说到整合度，揭示重要的线性连接的最好方法就是：在米制距离半径限制下，计算转角度数。当半径为n时，整合度的值就是系统中全局角度深度的倒数。诸多试验证明，用线段长度对整合度进行简单的加权，加权后结果大体上没有什么不同。因为当系统规模增大时，街道元素的结构值成对数正态分布，减小了平均值之间的差异。而选择度不适用该方法，这主要由于选择度通常呈现指数分布。

在规模较大的系统中，应用米制距离加权或角度加权时，选择度的结果似乎并不理想。事实上，路径上某个局部线段中某个看似微不足道的影响，都会作用于计算过程，并对系统总体表达产生负面影响。然而，受半径限制的选择度在分析网络流动性交通能力时，效果很理想，特别适用于米制距离加权。对选择度最好的加权方法是加权最短角度路径中的起点和终点（Hillier et. al., 2009）。用这种方法，通过加权起点线段和终点线段，使街区大小的变化也被考虑了进去。当在半径为n时，这种方法也许不是很有效。但是，计算最小转角角度比计算最短米制距离更有效。因此，不管是单独计算，还是合并计算，角度选择度和角度整合度分析在强调街道结构的前景网络时都是可靠的。